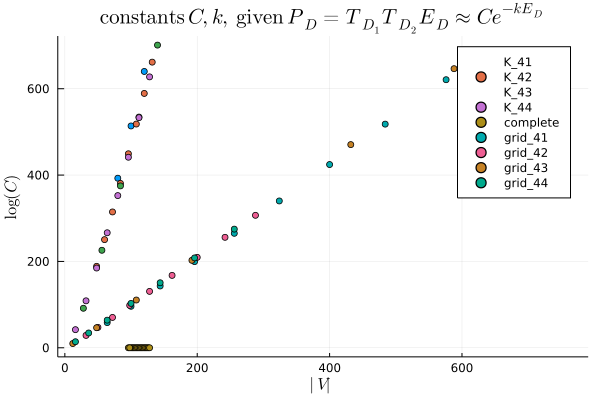
For my final project in Math 260, a graduate level special topics course in Markov chains Monte Carlo taught by Moon Duchin, I investigated various properties of random graph partitions by using Markov chain Monte Carlo sampling techniques. In particular, I attempted to quantify the relationship between cut edges and the number of spanning trees in the induced components. Recent research in this area found exponential relationships between certain quantities in a very specific class of graphs, and I was able to succesfully generalize these results to a greater set of graphs and find a particularly beautiful pattern that arises in the coefficients of certain exponential relationships.
The motivation for this type of research is applications to gerrymandering characterizations. If we are able to better understand the properties of random graph partitions, we will be able to better detect if a given redistricting plan is gerrymandered or random. What I showed can be used to determine how unlikely a certain districting plan is to occur randomly.
The motivation for this type of research is applications to gerrymandering characterizations. If we are able to better understand the properties of random graph partitions, we will be able to better detect if a given redistricting plan is gerrymandered or random. What I showed can be used to determine how unlikely a certain districting plan is to occur randomly.
Counting
2005
One of my seminal works was a project I completed for Kindergarten, an upper level elementary school class, focused on the fundamentals of number theory. Here, I performed an original analysis of the ring of integers in a succesful effort to gain experimental data on the closure of the additive group. I was able to derive various arithmetic identities in addition that have proven critical in subsequent developments in multiplication. The work was awarded a well done sticker, which is one of the most prestigious elementary school math awards.
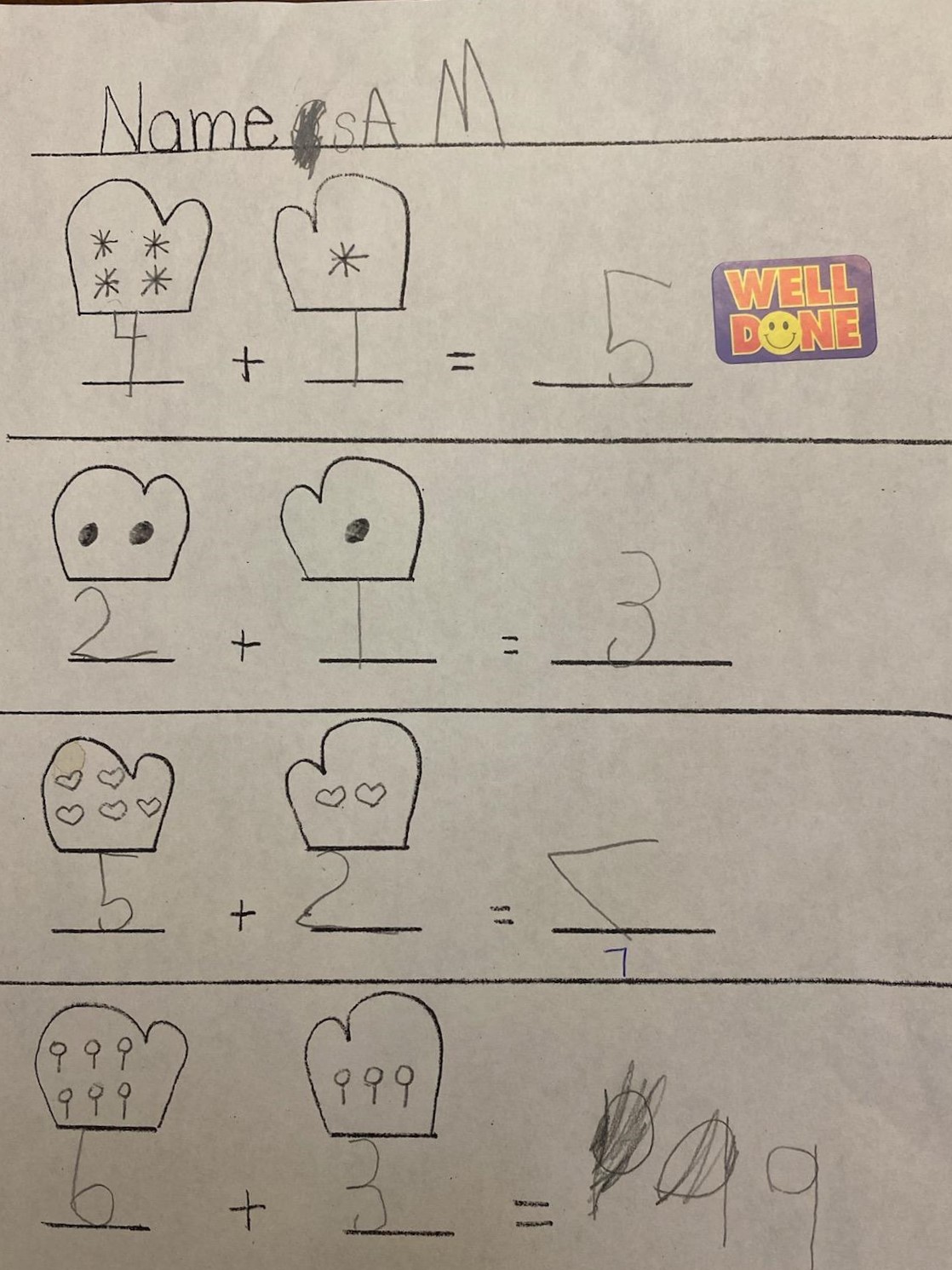
###